小学館の通信教育「名探偵コナンゼミ」を運営する小学館集英社プロダクションで、数々の保護者の学習周りのお悩みを解決してきた家庭学習のプロがお伝えする学習お悩み相談室。今回は、算数の文章題の苦手克服記事!算数の文章題の苦手克服のカギとなる重要ポイントや、算数の文章題を得意にするのにおすすめな教材を紹介します!
「この問題がわからない!」とお子さんに言われて解いている問題を覗くと算数の文章題だった、なんてことよくありませんか?
算数の文章題といえばただの計算問題とは違い「読んで理解するのがめんどくさい」「式を考えるのが難しい」などの理由で小学生の子どもたちから敬遠されがちな問題。単元自体は理解はしているものの、問われていることが正確につかめず不正解となることも。
算数の文章題が苦手!というお子さんへのアプローチとしてぜひ参考になさってください。
算数の文章題、苦手なまま放置するとどうなる?
文章題は計算問題と違って、たくさん練習すれば解き方が身につくものではありません。問題文に書かれている内容が理解できなければ答えが出せない問題です。
でも、中学以上の数学と違い、小学校の算数の文章題では、日常生活の場面を使われることが多いのが特徴。場面が具体的に設定されているので、その場面を読み取ってきちんとイメージすることで、問われていることがはっきりし、答えを求める方法も思い浮かべることができます。
場面をイメージすることはとても大事で、高学年になってからも必要なことですから、低学年のうちにしっかりと丁寧に練習しておきましょう。
文章題を解くには「イメージする力」や「読解力」だけでなく「計算する力」「立式する力」なども必要です。
「今はまだ文章題が苦手だから」「もうすこし読解力がつけば何とかなると思うから」とそのままにしておくと、苦手意識が強くなってしまいます。
学年が上がるにつれて問題文は長くなり、個数や単位などの条件も複雑になっていきます。そのため「文章題が苦手」から「文章題なんて大嫌い!」になってしまうお子さんをたくさん見てきました。お子さんのテストの答案や宿題のプリントなどから「文章題が苦手なのかな?」と感じることがあったら、なるべく早く原因を探って克服しておきましょう。
得意な子と苦手な子はここが違う!
「文章題が得意、楽しい!」というお子さんたちにはいくつかの共通点があります。
それは、問題文を正しく読み取る力だけでなく、読み取った場面をイメージして絵や図に落とし込むことができるということです。
問題文の場面を絵としてとらえることができると、どんな式を立てたらいいのかも自然な流れで思い浮かべることができます。なにより、絵や図に表すことができると頭の中にある情報が整理されます。低学年のころから、問題文を絵や図に表して考える練習をしておくと、高学年になって複雑な問題に取り組むときに役立ちます。
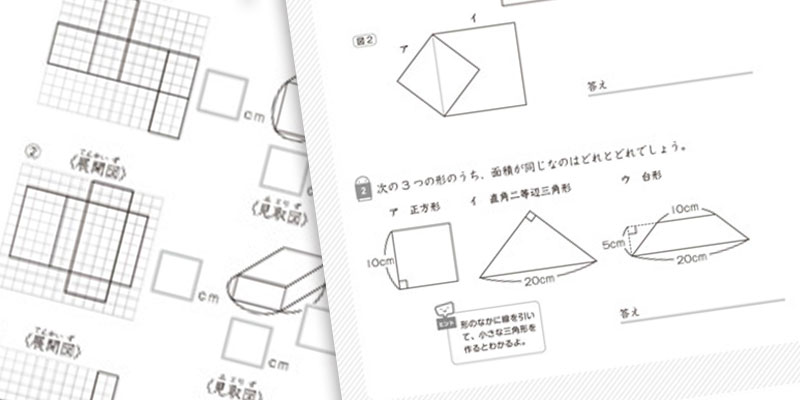
また、算数の文章題を解くためには、国語の力も必要とされます。文章題が苦手なお子さんは「本を読むことがあまり得意でない」「意味が分からない言葉などを調べることを面倒に感じてしまう」など読解や語彙の学習を苦手に感じられていることもあります。
そのため、「どんな問題なの?」と聞くと要領を得ない説明になりがちです。そんな時はいくつか補正的な質問(いくつもらったの? 残りが知りたいのね、など)をしてお子さんの頭の中で順番に整理できるようにさせてあげるといいでしょう。
実際に式を立てるときには手を動かすこともお勧めします。
「どちらがどれだけ多いでしょう」という問題であれば、おはじきやキャンデーなど身近にあるものを使って、お子さん○個、おうちのかた△個と問題文どおりに分けてみて、「どっちが多いかな?」と考えてみましょう。手を使っておはじきなどを動かしてみると、正解を導けるはずです。このように問題文に書いてある順に行動すると、どんな式に表すかイメージができ立式ができます。そして、問題文に出てくる数字の順序などに惑わされることはなくなります。
それから、問題文を声に出して読むことも有効。大事なところに線を引きながらゆっくりと読んでください。低学年では、問題文の後半を読むころには前半部分がもう頭からぬけてしまっているということがよくあります。線を引いておくと必要なところだけが目にとびこんでくるようになりますね。手を使って作業をしながら読むことで、落ち着いて考えることができるという効果もあります。
学年別の攻略ポイント!
それでは、次に学年別におさえておきたいポイントをご紹介していきます。
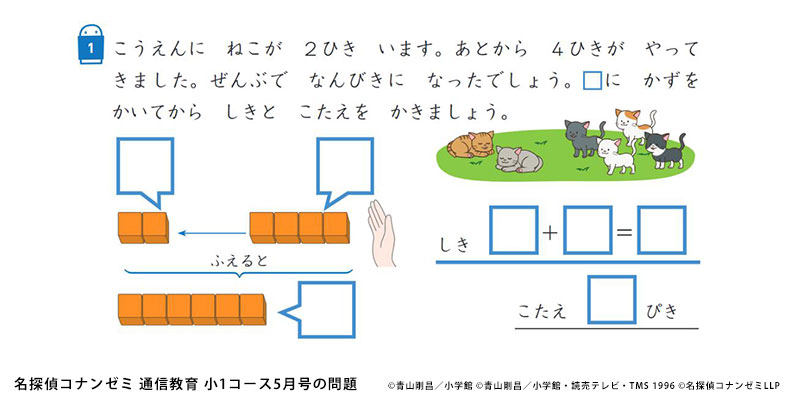
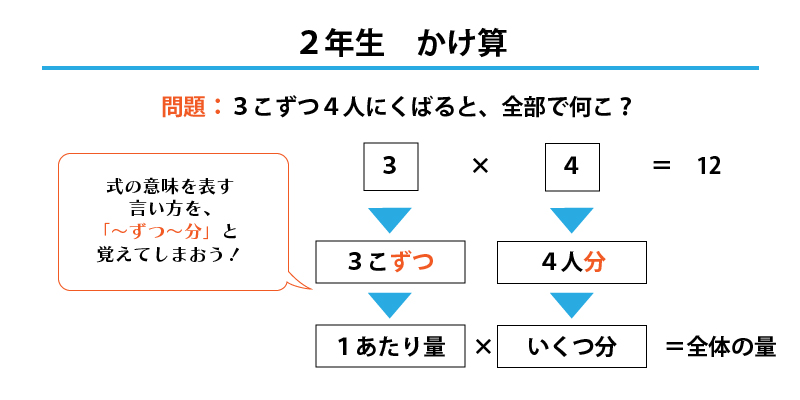
【1年生】物語文のストーリーをつかもう!
問題文にはストーリーがあるので、そのストーリーに沿って数の変化を再現しましょう。おはじきやタイルを用意しておいて問題文を読みながらおはじきやタイルを動かして、数の変化を目で確かめると、「もらうと数は増える」「あげると数は減る」という発見があると思います。
数が増える→たし算、数がへる→ひき算という理解に結びついていきますよ。
ひき算には、「残りを求める」「差を求める」「補う数を求める※」の3種類があることも練習を繰り返して理解しておきましょう。差を求める場合は「どちらが どれだけ 多い(少ない)」など答え方にも注意が必要な問題があります。
※求補といい、全体の数と一部の数が分かっている場合に他方を求める計算です。(例)「トランプが10枚あります。そのうち黒いマークのカードは3枚です。赤いマークのカードは何枚でしょう。」
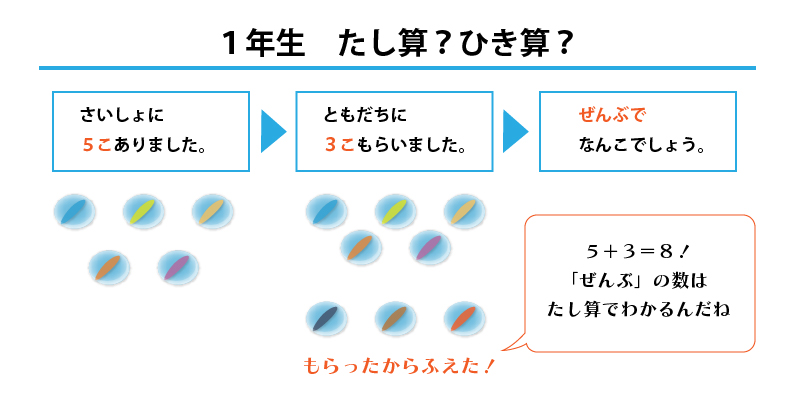
【2年生】かけ算の式は「1あたり量」×「いつくぶん」=「全体量」
「3個ずつ4人に配ると全部で何個でしょう」
という問題では「3×4」が「3個ずつ4人分」となり正解です。「4×3」では「4人ずつ3個分」という間違った意味の式になってしまいます。
式の意味を分かりやすくするために「○ずつ△分」といういい方にあてはめるときは問題文と同じ単位をつけて「○個ずつ△人分」「○ページずつ△日分」などと確認するとよいでしょう。
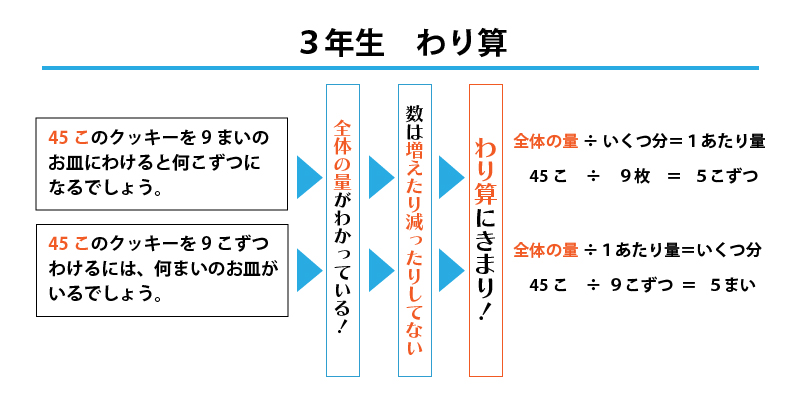
【3年生】わり算の問題なのにかけ算やたし算の式を立ててしまわないように…!
わり算は「分けるときに使う」計算です。問題文の「分ける・配る」「~ずつに切る・~ずつ入れる」などの言葉から、2年生で覚えた「1あたり量×いくつ分」を連想してかけ算だと早合点してしまいがちです。
わり算の文章題では「全体量」はわかっていることを覚えておきましょう。問題文に全体量が書かれていれば、かけ算を使って解く問題ではないのです。
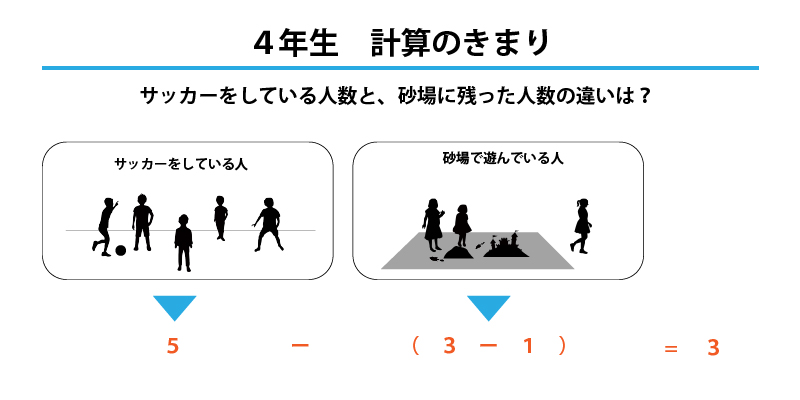
【4年生】計算のきまりを使って式を立てる!
「公園で5人の子どもがサッカーで遊び、3人の子どもは砂場で遊んでいました。砂場にいる3人のうち1人が家に帰ったら、サッカーをしている子と砂場にいる子の違いは何人でしょう。」
という問題では、砂場に残った人数を「3−1」で求め、サッカーをしている人数から砂場に残った人数を引かねばなりません。「5−3−1」と立式してしまうと全く違う数を求める計算になってしまうので、ここでは( )を使った式を立てる必要がありますね。
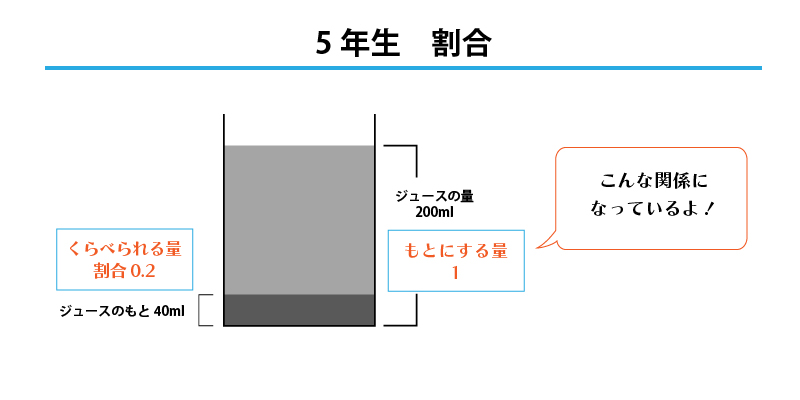
【5年生】割合は、くらべられる量÷もとにする量 で求めよう!
割合は難しく感じるお子さんが多い単元です。
「200mLのジュースを作ります。ジュースのもとを0.2の割合で混ぜる場合、ジュースのもとは何mL必要ですか。」
このとき割合は0.2、作りたいジュースの量が「もとにする量」、ジュースのもとの量が「比べられる量」になります。「割合=比べられる量÷もとにする量」をしっかり覚えて式を立てましょう。
0.2=□÷200 となるので
□は
200×0.2=40 で求められます。
なにが「比べられる量」で、何が「もとにする量」なのか、文章や図から読み取る練習を繰り返しておきましょう。
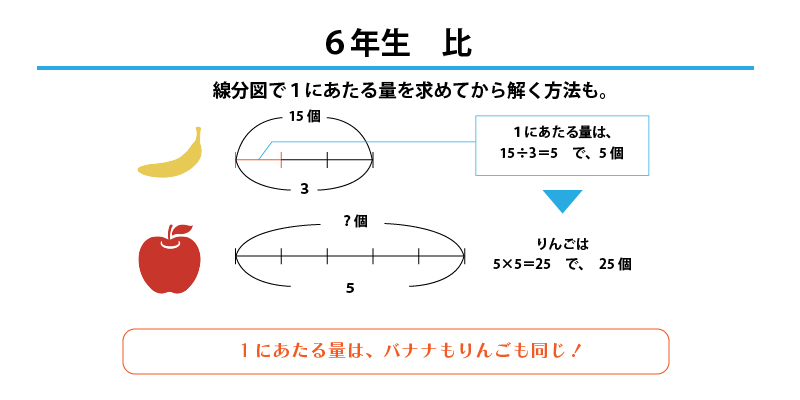
【6年生】比を使った文章題
比の出し方や比の値については機械的にだすことができるので取りつきやすいのですが、具体的な数量が出てくる問題になると難しく感じるお子さんが多いようです。
「バナナとりんごの数の比は3:5です。バナナの数は15個です。りんごは何個でしょう。」
という問題の場合、比を作っている順序を間違えないようにして線分図を書いてみましょう。比の1にあたる量はバナナもりんごも同じなので1にあたる長さを決めて線分図にします。バナナの数の15個も書き入れておきましょう。するとバナナの部分から1にあたる量が分かります。
比のしくみが分かると、ひとしい比を利用して「3:5=15:□」で求めることができるようになりますよ。
算数の文章題が得意になる名探偵コナンゼミ!その特長は??
名探偵コナンゼミでは、文章題を「図」に表すことで場面を理解し、迷わずに立式できる力を伸ばしていきます。
学年、学習内容に応じて「ブロック図」「テープ図」「線分図」などの図を系統的に使用できるよう学習カリキュラムを組み立てています。系統的に繰り返し取り組むことで、「計算は得意だけど文章題はちょっと苦手かも」というお子さまの苦手を克服します。
またこれにより、どんな道すじで答えにたどりついたか、説明できる力にもつながりどのような問題にも対応できる本質的な理解を深めていきます。
©青山剛昌/小学館 ©青山剛昌/小学館・読売テレビ・TMS 1996 ©名探偵コナンゼミLLP
著者プロフィール

- 石山絵麻 先生
- 小学館集英社プロダクション コンテンツ開発室所属。長年、教育事業に関わり、数々の保護者の学習周りのお悩みを解決してきた家庭学習のプロ。